Download paper: [cvpr2011.pdf], video demo: [demo.avi], presentation: [slides].
 Data and code for convex learning:
[emp_code.zip].
Data and code for convex learning:
[emp_code.zip].

Gloria Zen Ph.D.
| Home | Research | Publications | Datasets |
| >> EMD |
|
We present a novel approach for automatically discovering spatio-temporal patterns in complex dynamic scenes.
Similarly to recent non-object centric methods, we use low level visual cues to detect atomic activities and then construct clip histograms.
Differently from previous works, we formulate the task of discovering high level activity patterns as a prototype learning problem
where the correlation among atomic activities is explicitly taken into account when grouping clip histograms.
Interestingly at the core of our approach there is a convex optimization problem which allows us to efficiently extract patterns at multiple levels of detail.
The effectiveness of our method is demonstrated on publicly available datasets.
Download paper: [cvpr2011.pdf], video demo: [demo.avi], presentation: [slides].  Data and code for convex learning:
[emp_code.zip]. Data and code for convex learning:
[emp_code.zip].

|
Readme.txt
Problem formulationGiven a set of histogramswe aim to learn N representative prototypes where D is the number of atomic activities. This task is formalized as a convex optimization problem: 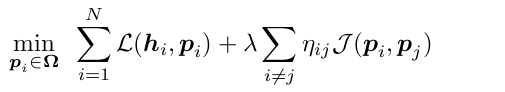
where: Loss: similarity between prototype pi and associated histogram hi Regularization: smoothness among neighboring prototypes ( pi is fused into pj ) ηij = {0, 1} indicates prototype's neighborhood. An efficient variation of the Earth's Mover Distance (EMD) is adopted in the Loss. This allows to consider similarity between atomic activities when comparing histograms. In practise...Given a set of histograms, it is possible to obtain a multiscale clustering by simply varying the value of parameter λ.(see sample figure below, with N=4 and D=8) 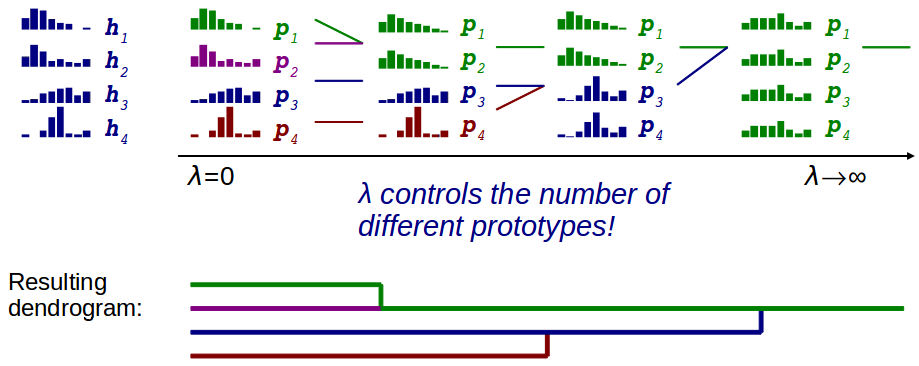
|