Python: Functions¶
Functions are named blocks of code. They take inputs and produce outputs.
The abstract syntax is:
def function(arg1, arg2, ...):
# the code
return result
Once a function is defined (as above), it can be called as follows:
the_result = function(value1, value2, ...)
The arguments (arg1, arg2, etc.) are variables that specify how many
inputs the function takes. The variable result is output from the function
to its caller.
Warning
The name of the variables I pass to the function has nothing to do with the name of the arguments.
In the code above, the values of the variables
valueXare visible from the inside the function asargX:arg1takes the value ofvalue1arg2takes the value ofvalue2- etc.
The name of the variable I use to store the result of the function has nothing to do with the name of the variable used inside the function to store the result.
In the code above, the value of the result is stored in the
resultvariable inside the function, but is stored inside thethe_resultvariable by the caller.the_resulttakes the value ofresult
Example:
def function(a, b):
r = a + b
return r
x = 5
y = 10
z = function(x, y)
print z
Here a takes its value from x, b from y; return r
makes the function return the value of r, which is assigned by the
caller to the variable z.
Example. Let’s define a function that takes two numbers and returns their sum:
def add(n, m):
return n + m
It can be used as follows:
result = add(4, 6)
print result # 10
result = add(6, 4)
print result # 10
By replacing the calls to add() with the code in the definition of the
add function, and substituting the arguments with the input values, we get
the equivalent code:
n = 4
m = 6
result = n + m
print result # 10
n = 6
m = 4
result = n + m
print result # 10
As with all Python-provided functions, I can also skip assigning the return
value to a variable (result in the code above):
print add(4, 6) # 10
Example. Let’s write a function print_sum() that prints the sum of
two numbers:
def print_sum(n, m):
print n + m
It can be used as follows:
print_sum(4, 6) # prints 10
print_sum(6, 4) # prints 10
Warning
Notice that there is no return statement in print_sum().
When return is omitted, the function automatically returns None:
result = print_sum(4, 6) # prints 10
print result # prints None
Warning
A function does nothing until it is called.
Consider the Python module test.py:
print "beginning"
def function():
print "I do stuff"
print "end"
Running it with the Python interpreter:
$ python test.py
produces the following output:
beginning
end
As you can see, the interpreter executes the code line by line. However,
while the function function() is defined in the middle of the module,
it is not called anywhere. Therefore it is not executed at all.
In order to actually call the function, let’s write:
print "beginning"
def function():
print "I do stuff"
function()
print "end"
This code prints:
beginning
I do stuff
end
as expected.
Example. Let’s write a function factorial() that computes the factorial
of an integer n:
Now, let’s compute the factorial of n normally (i.e. without defining
a new function):
fact = 1
for k in range(1, n + 1):
fact = fact * k
Now that we have the code for computing the factorial, it is easy to write a function that computes the factorial: it is sufficient to plug the above code inside a new function, as follows:
def factorial(n):
fact = 1
for k in range(1, n + 1):
fact = fact * k
return fact
And let’s check if it works:
print factorial(1) # 1
print factorial(2) # 2
print factorial(3) # 6
print factorial(4) # 24
print factorial(5) # 120
print factorial(6) # 720
Of course, the new function can be used like any of the Python-defined functions, e.g. in list comprehensions:
factorials = [factorial(n) for n in range(10)]
Warning
The name of the function, as well as the name of the arguments, are arbitrary: pick whichever name you find more fitting.
Quiz. What is the difference between this code:
def arith(op, a, b):
if op == "+":
return a + b
elif op == "*":
return a * b
else:
return None
print arith("+", 10, 10)
print arith("*", 2, 2)
and this code?:
def f(what, x, y):
if what == "+":
return x + y
elif what == "*":
return x * y
else:
return 0
print f("+", 10, 10)
print f("*", 2, 2)
Note
A function can return more than one result, as follows:
def multiresult():
result_1 = "first result"
result_2 = 0.12
result_3 = "something else"
return result_1, result_2, result_3
Internally, Python interprets the return statement as returning
a tuple. In practice, the above code is equivalent to:
def multiresult():
return ("first result", 0.12, "something else")
When I call a “multi-result” function, I can either put the resulting tuple into a variable and extract the various elements individually:
result = multiresult()
res1 = result[0]
print res1
res2 = result[1]
print res2
res3 = result[2]
print res3
or I can use the “automatic unpacking” feature of Python, as follows:
res1, res2, res3 = multiresult()
print res1
print res2
print res3
Warning
Variables have a scope, and in particular:
Variables declared outside the function are not visible the inside. [1]
If you want to pass one or more values from the outside to the function, pass them through the arguments.
Variables declared inside the function are not visible from the outside.
If you want to pass one or more values from the function to the external world, use the
returnstatement.
[1] There are exceptions to this rule; we will ignore them in this presentation.
Exampe. Consider this code:
def find_physical(triples):
"""Takes a mixed interaction protein network, example:
[("1A3A", "physical", "5ARM"),
("5JTD", "genetic", "5TGD")]
and extracts physical interacting protein pairs, example:
[("1A3A", "5ARM")]
"""
phys_pairs = []
for p1, relation, p2 in triples:
if relation == "physical":
phys_pairs.append((p1, p2))
# XXX I forgot to return `phys_pairs` here!
network = [
("1A3A", "physical", "5ARM"),
("5JTD", "genetic", "5TGD")
]
find_physical(network)
print phys_pairs
Here phys_pairs is declared inside the function: it is not visible
from the outside!
In order to fix this issue, I have to explicitly return it:
def find_physical(triples):
phys_pairs = []
for p1, relation, p2 in triples:
if relation == "physical":
phys_pairs.append((p1, p2))
return phys_pairs
network = [
("1A3A", "physical", "5ARM"),
("5JTD", "genetic", "5TGD")
]
result = find_physical(network)
print result
Example. Functions can call other functions. Let’s write two functions:
def read_fasta(path):
"""Reads a FASTA file with one-line sequences."""
fasta = {}
for line in open(path).readlines():
line = line.strip()
if line[0].startswith(">"):
header = line
else:
fasta[header] = line
return fasta
def compute_histogram(sequence):
"""Computes the histogram of the characters."""
histogram = {}
for letter in sequence:
if not histogram.has_key(letter):
histogram[letter] = 0
histogram[letter] += 1
return histogram
These functions can be used to implement a complex program that:
- Reads a FASTA file into a dictionary
- For each sequence in the FASTA file, computes the histogram of its letters
- Prints each sequence header and the corresponding histogram
as follows:
path = raw_input("enter a path: ")
fasta = read_fasta(path)
for header, sequence in fasta.items():
histogram = compute_histogram(sequence)
print "header =", header.lstrip(">"), ":"
print histogram
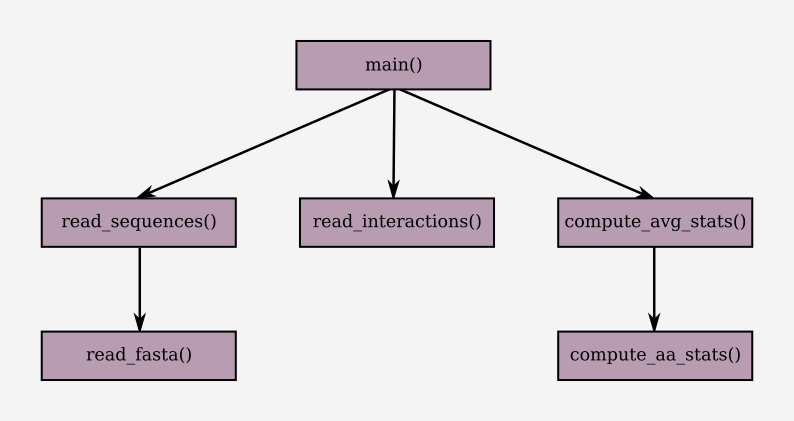
Example. Since functions can call other functions, the “call graph” of a program can become arbitrarily complicated. Let’s see a moderately realistic example of what a call graph looks like.
Let’s write a (mock!) program, composed of multiple functions, that asks the user for:
- the path to one or more FASTA files.
- the path to a file describing a physical protein interaction network (PIN).
and computes some average statistic (say, a histogram) of the amino acid composition of interacting proteins.
When ran, the program does the following:
- reads the sequence data from each FASTA file, see the
read_sequences()andread_fasta()functions - reads the interaction network with the
read_interactions()function - for each pair of interacting proteins, computes statistics about their
joint amino acid composition, through the
compute_aa_stats()function, and computes an “average” summary statistic in thecompute_avg_stats()function.
Here is the code:
def read_fasta(path):
"""Takes a path to a FASTA file, returns a
header->sequence dict."""
# TODO actually read the file
return "1A3A:A", "MANLFKLG..."
def read_sequences(paths):
"""Reads a bunch of FASTA files, returns a
list of dicts."""
header_to_seq = {}
for path in paths:
header, seq = read_fasta(path)
header_to_seq[header] = seq
return header_to_seq
def read_interactions(path):
"""Reads physical protein interactions from a
file. Returns a list of pairs of strings."""
# TODO actually read the file
return [("1A3A:A", "5AA3:F"), ("5AA3:F", "5K9C:A")]
def compute_aa_stats(seq1, seq2):
"""Compute amino acid statistics, e.g.
co-occurrence."""
# TODO actually compute co-occurrence and MI
cooccurrence = {"A": 0.2, "C": 0.01}
mutual_information = 0.72
return cooccurrence, mutual_information
def compute_avg_stats(sequences, interactions):
"""Takes a list of statistics (in some format) and
computes the average statistics."""
stats = []
for prot1, prot2 in interactions:
if not (sequences.has_key(prot1) and sequences.has_key(prot2)):
continue
seq1 = sequences[prot1]
seq2 = sequences[prot2]
stats.append(compute_aa_stats(seq1, seq2))
# TODO actually average all the collected statistics
return 0.3
def main():
"""The whole (fake) program."""
# Read the sequence files
paths = []
while True:
ans = raw_input("path to FASTA file: ")
if len(ans) == 0:
break
paths.append(ans)
sequences = read_sequences(paths)
# Read the interaction file
ans = raw_input("path to interaction data: ")
interactions = read_interactions(ans)
# Print the average stats
print "average stats =", compute_avg_stats(sequences, interactions)
main()
As you can see, Python begins by calling the main() function at the very
last line of the program. The main() function calls all the other
“major” functions: read_sequences(), read_interactions() and
compute_avg_stats().
The read_sequences() function internally calls the read_fasta()
function multiple times, once for each user-provided FASTA file.
The read_interactions() function calls no other function.
The compute_avg_stats() function uses the compute_aa_stats() function
to compute the statistics of individual protein-protein pairs.
The above can be summarized using a “call graph” like this:
Quiz. How many times is:
- the main() function called?
- the read_fasta() function called?
- the compute_aa_stats() function called?