LOGICAL MODELING - SLIDE
01

LOGICAL MODELING - SLIDE 02

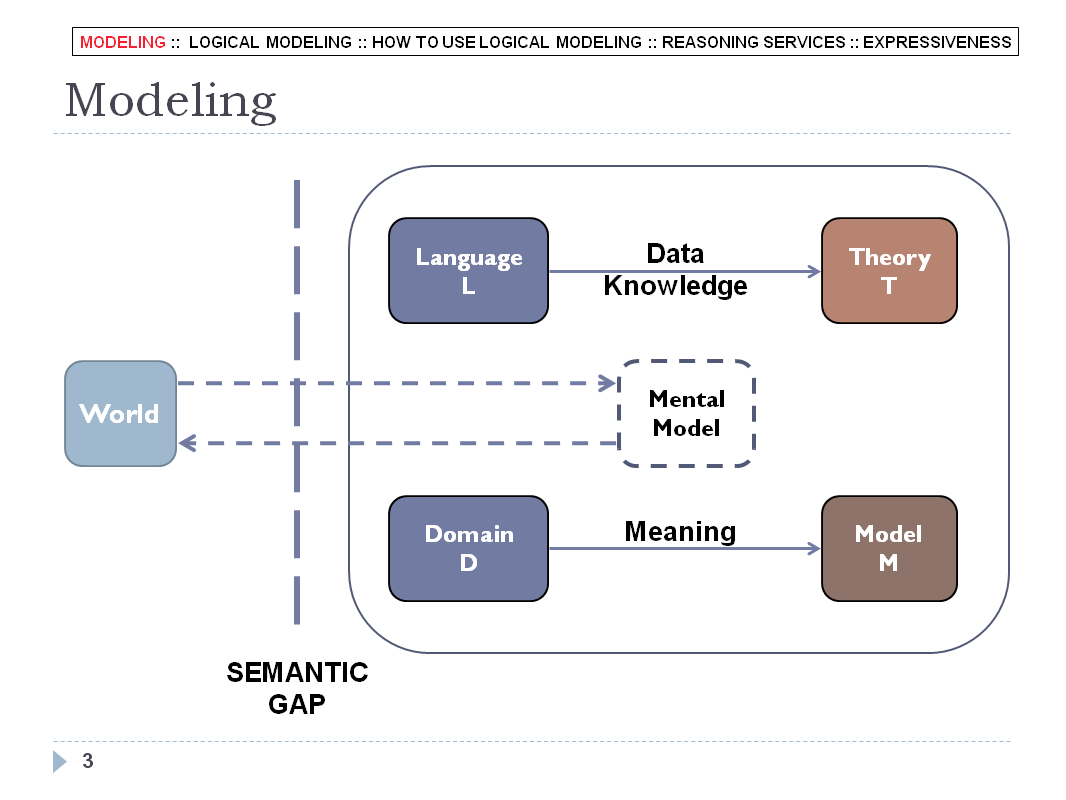
LOGICAL MODELING - SLIDE 03
LOGICAL MODELING - SLIDE 04

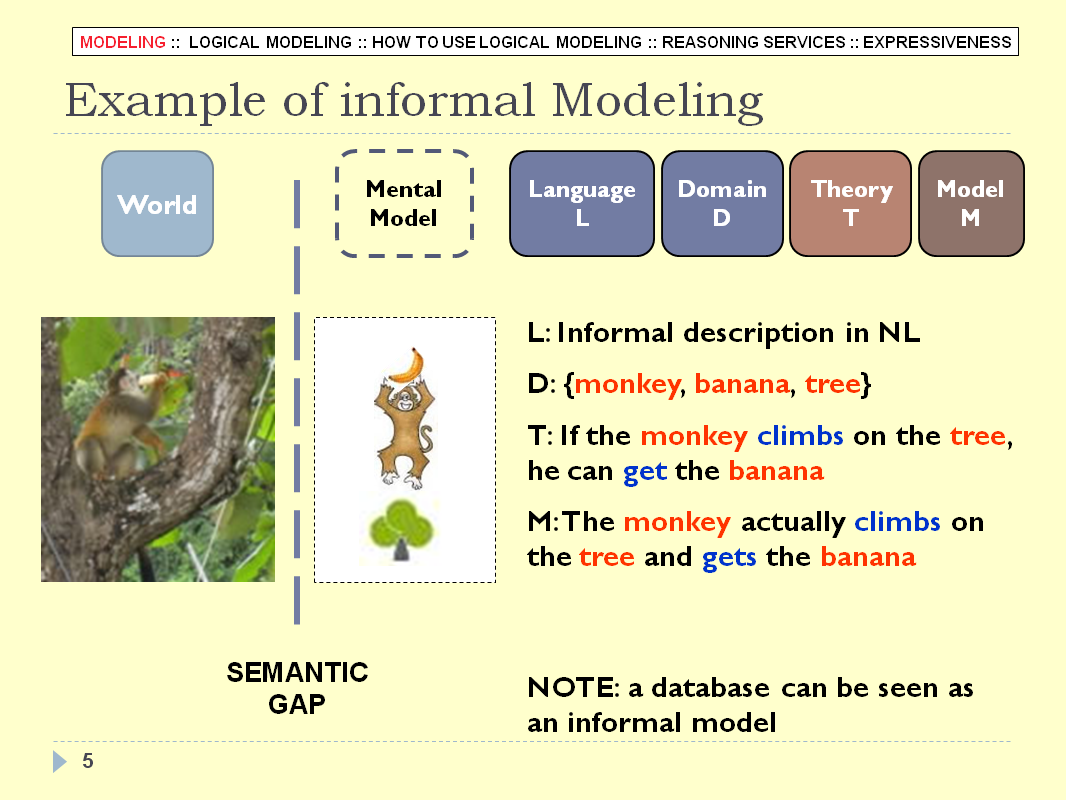
LOGICAL MODELING - SLIDE 05
LOGICAL MODELING - SLIDE 06

Looking at the slide someone could ask "is the Natural
Language decidable"? Without any sort of restriction, the NL is
NOT DECIDABLE and there are no ways to reach this property.
Using the Godel numbering by which encodes any formal
language in the set of naturals number, and the Godel's Theorem
of Incompleteness, there is always at least one "True sentence"
that cannot be stated True or False within the formal language
itself nor in ITS NATURAL INTERPRETATION.
References:
http://en.wikipedia.org/wiki/Gödel%27s_incompleteness_theorem
LOGICAL MODELING - SLIDE 07

LOGICAL MODELING - SLIDE 08
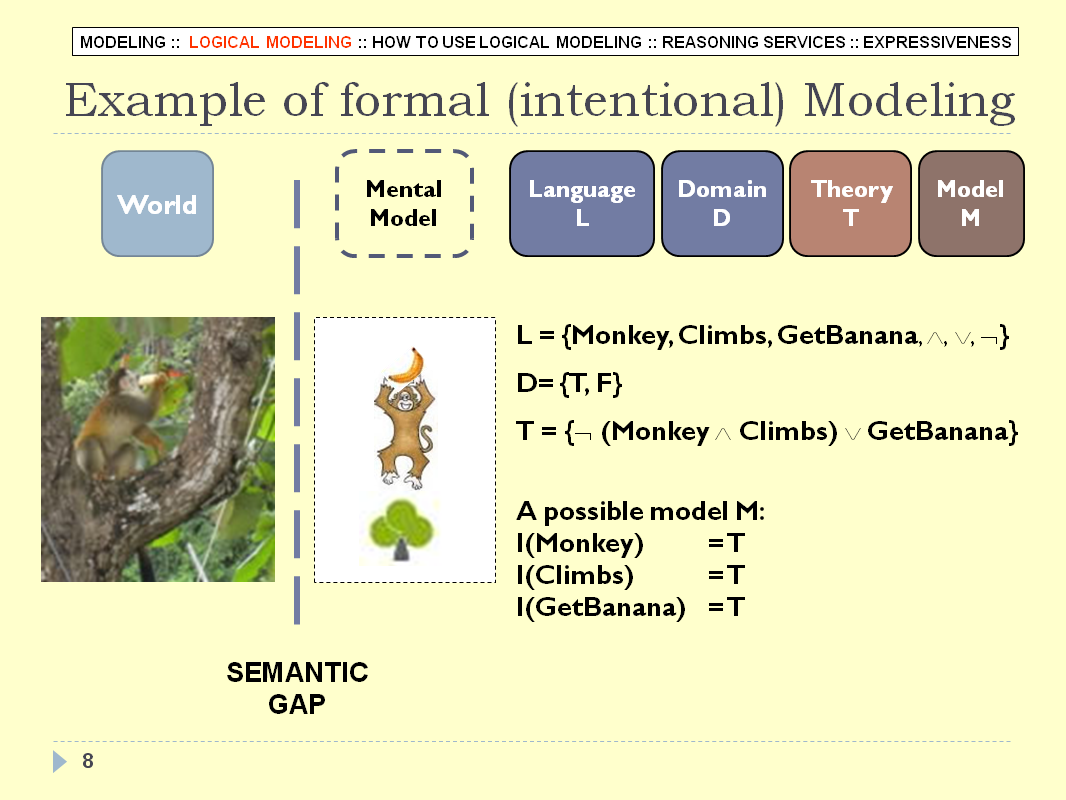
LOGICAL MODELING - SLIDE 09
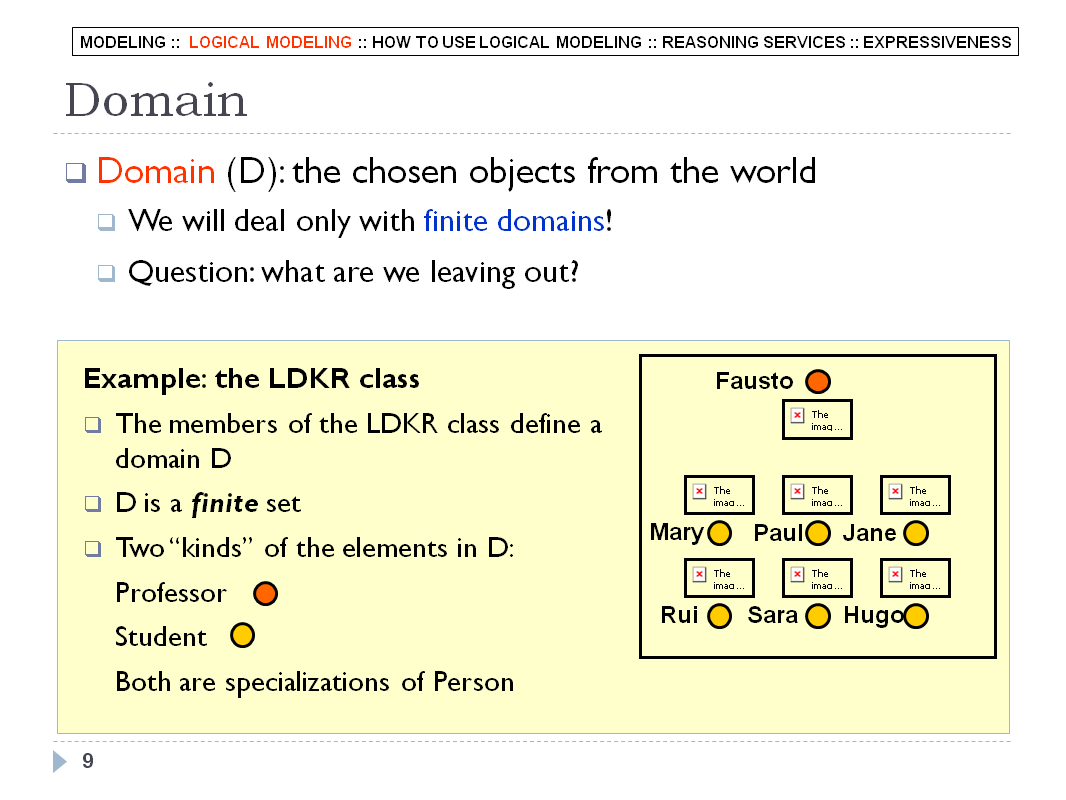
LOGICAL MODELING - SLIDE 10

LOGICAL MODELING - SLIDE 11

LOGICAL MODELING - SLIDE 12

LOGICAL MODELING - SLIDE 13

The following is related to the previous slide:
http://www.infitt.org/ti2003/papers/19_raman.pdf
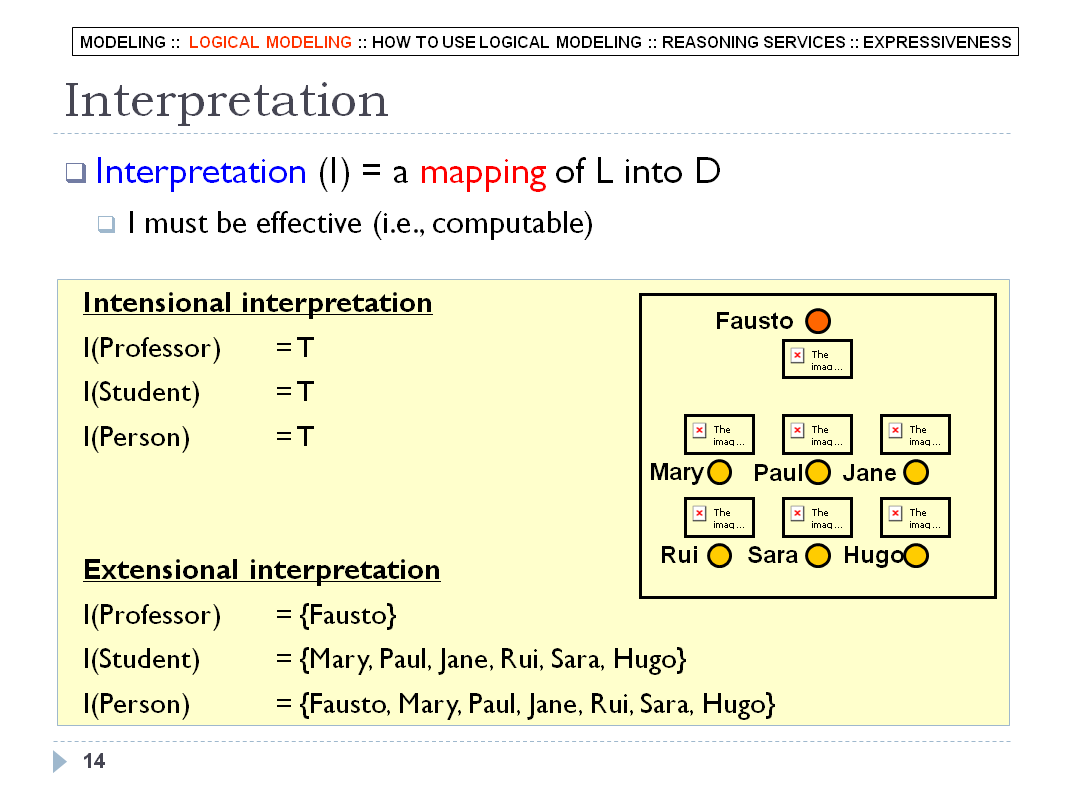
LOGICAL MODELING - SLIDE 14
LOGICAL MODELING - SLIDE 15

LOGICAL MODELING - SLIDE 16

LOGICAL MODELING - SLIDE 17

LOGICAL MODELING - SLIDE 18

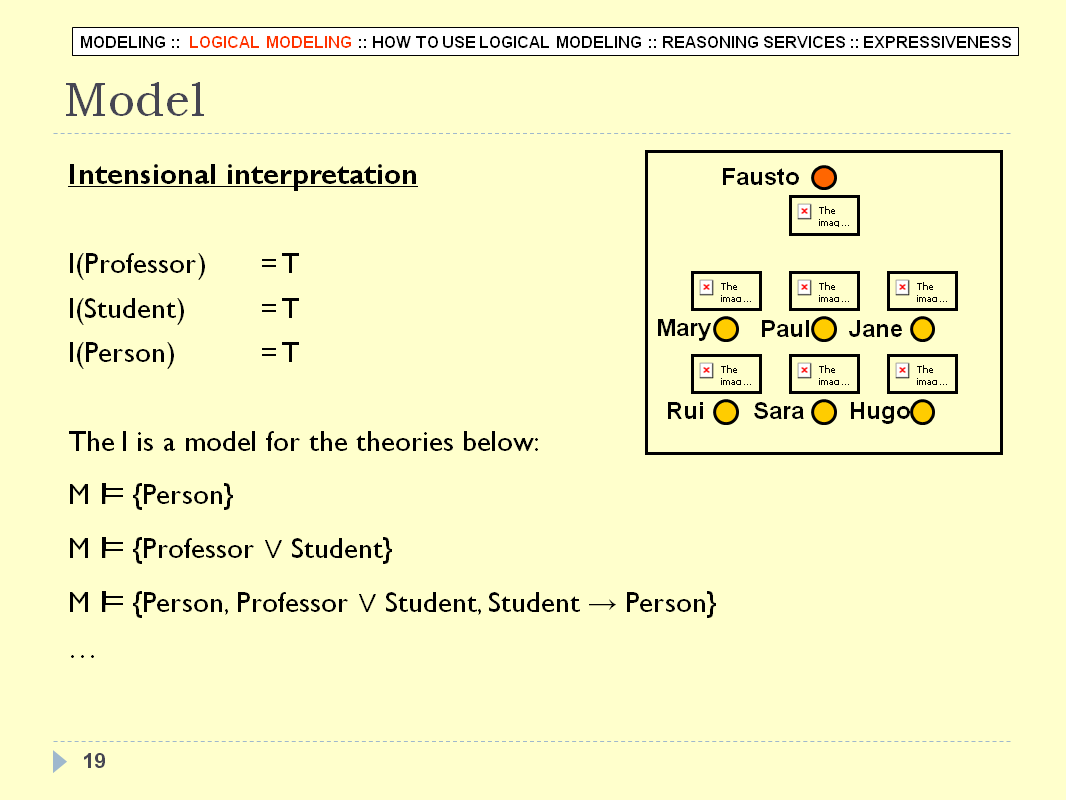
LOGICAL MODELING - SLIDE 19
LOGICAL MODELING - SLIDE 20

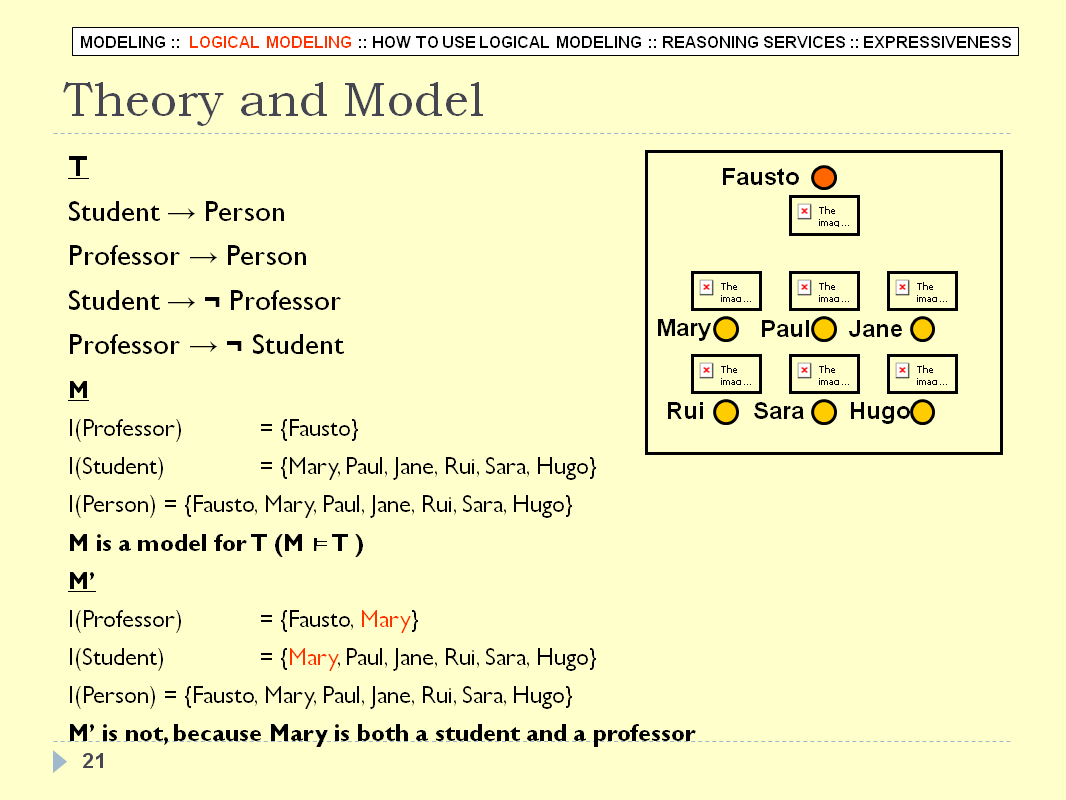
LOGICAL MODELING - SLIDE 21
LOGICAL MODELING - SLIDE 22

LOGICAL MODELING - SLIDE 23

LOGICAL MODELING - SLIDE 24

The last interpretation function of the formal semantics box
"I(MonkeyGetBanana) = F" should not be false. It should be
true
LOGICAL MODELING - SLIDE 25

LOGICAL MODELING - SLIDE 26

LOGICAL MODELING - SLIDE 27

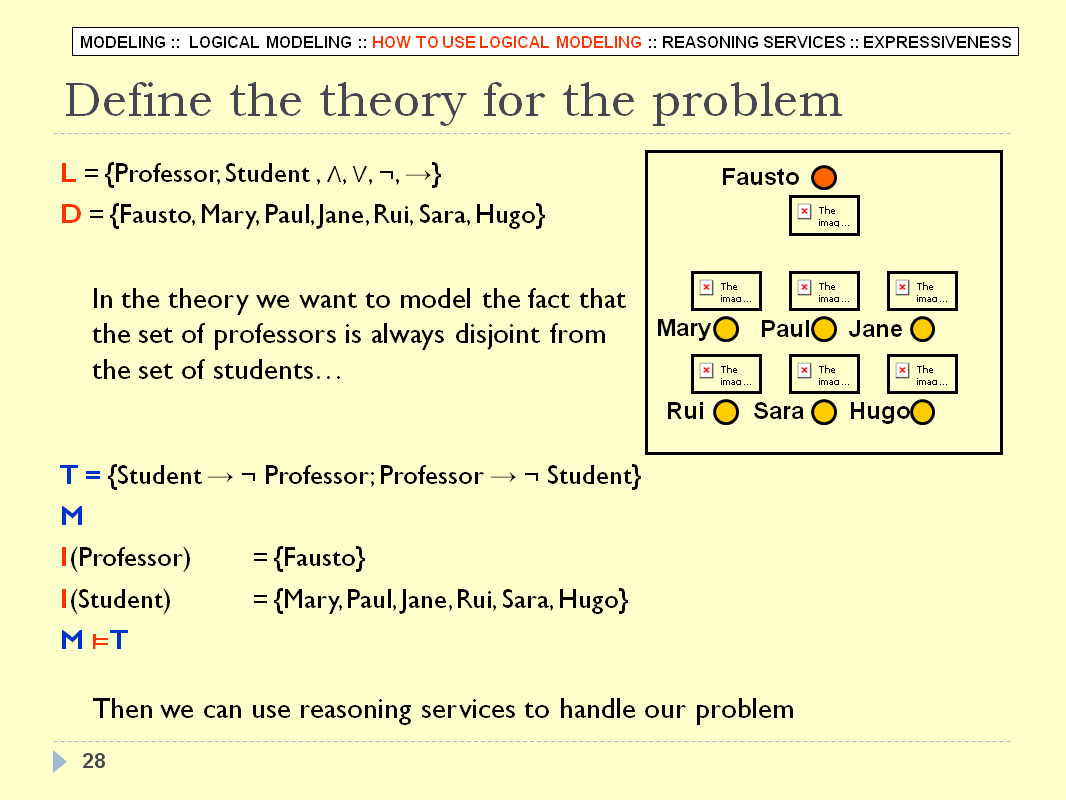
LOGICAL MODELING - SLIDE 28
LOGICAL MODELING - SLIDE 29

LOGICAL MODELING - SLIDE 30

LOGICAL MODELING - SLIDE 31
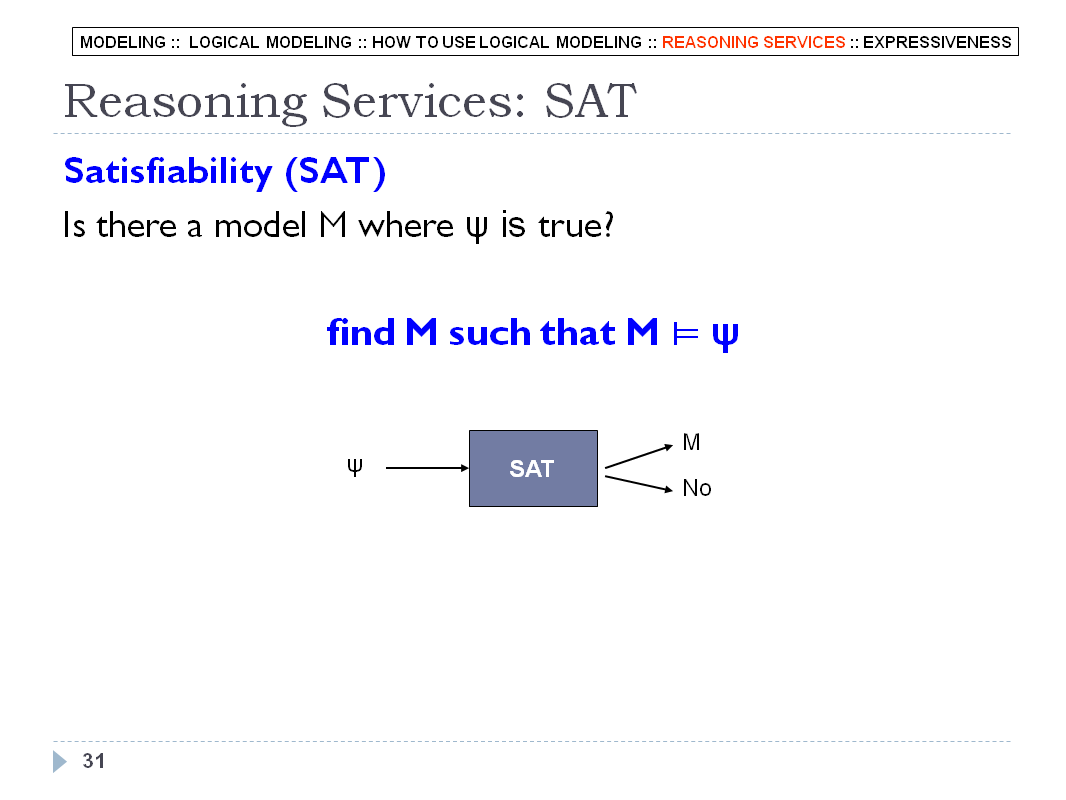
LOGICAL MODELING - SLIDE 32
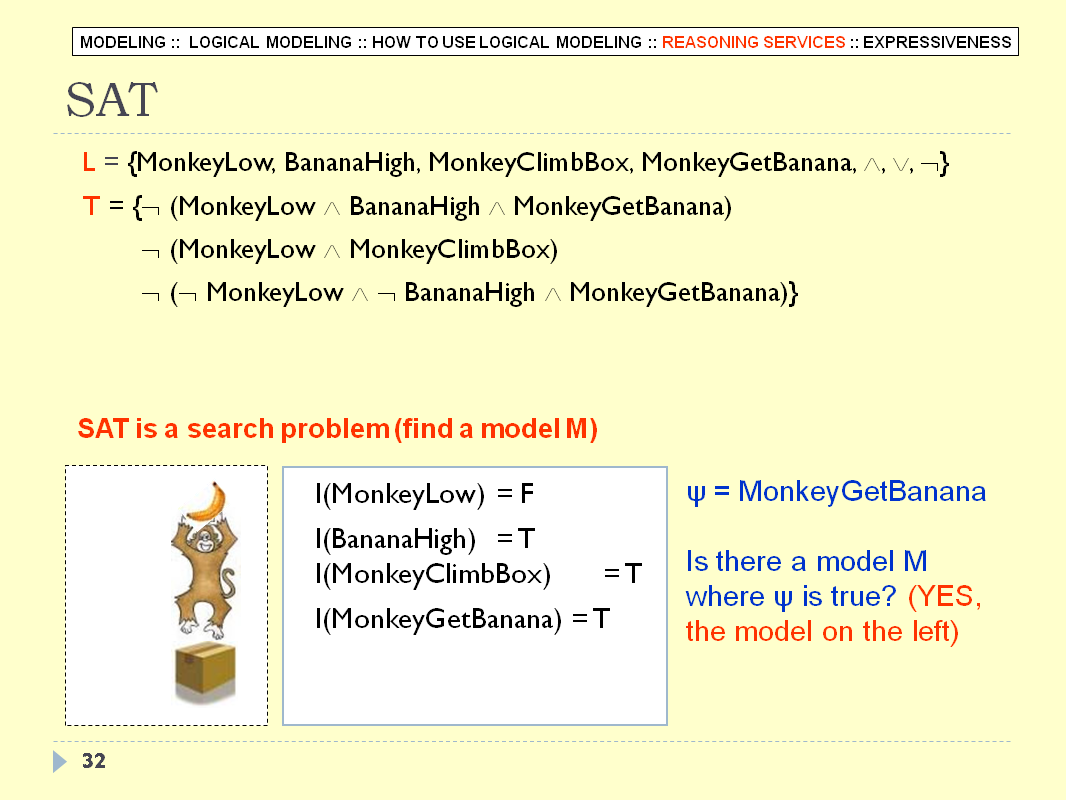
LOGICAL MODELING - SLIDE 33

LOGICAL MODELING - SLIDE 34
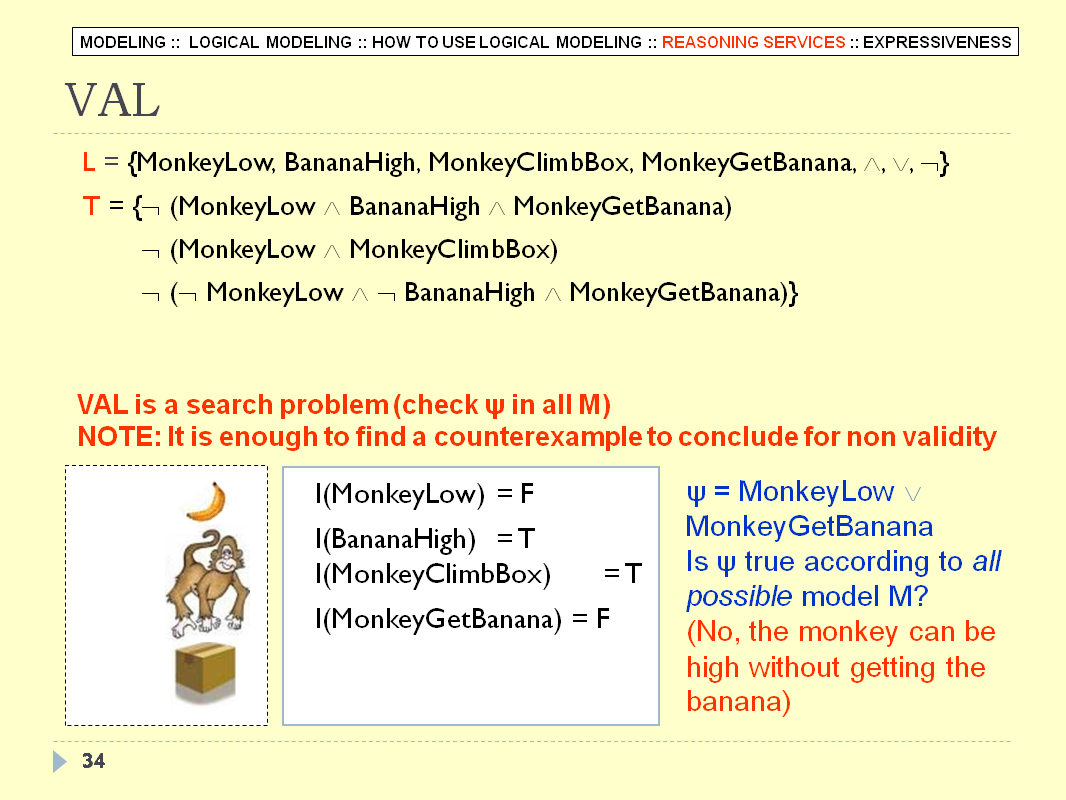
LOGICAL MODELING - SLIDE 35

LOGICAL MODELING - SLIDE 36
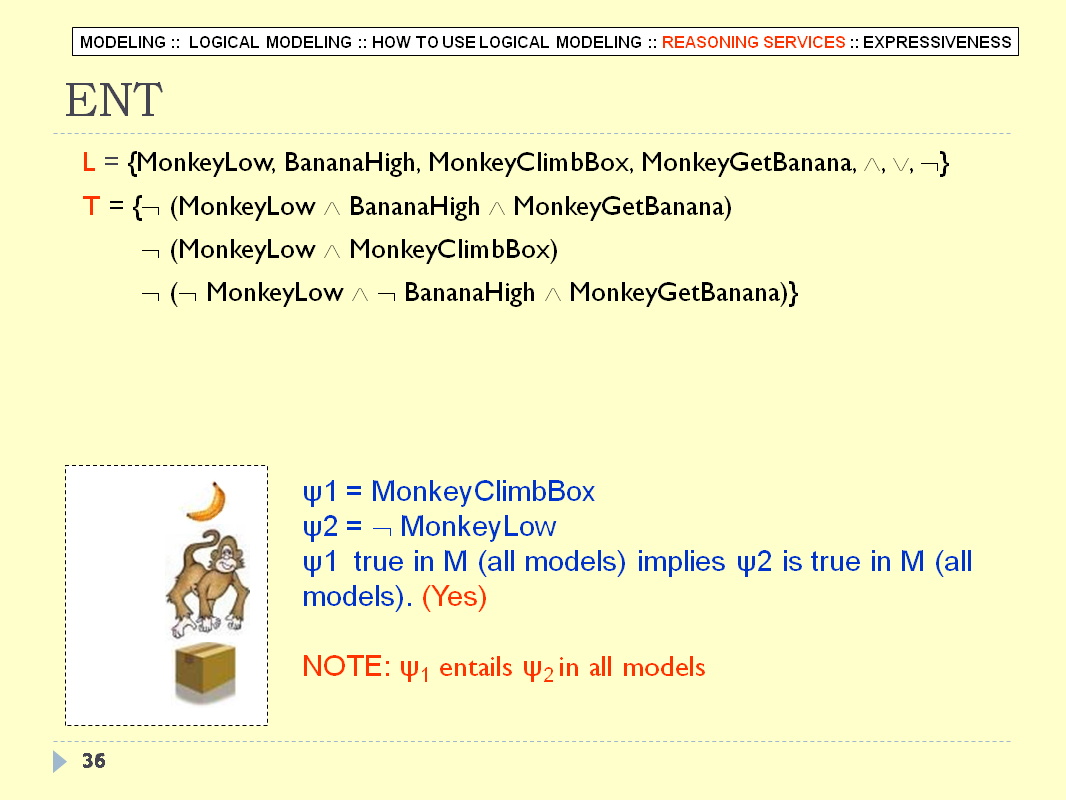
LOGICAL MODELING - SLIDE 37

LOGICAL MODELING - SLIDE 38

LOGICAL MODELING - SLIDE 39

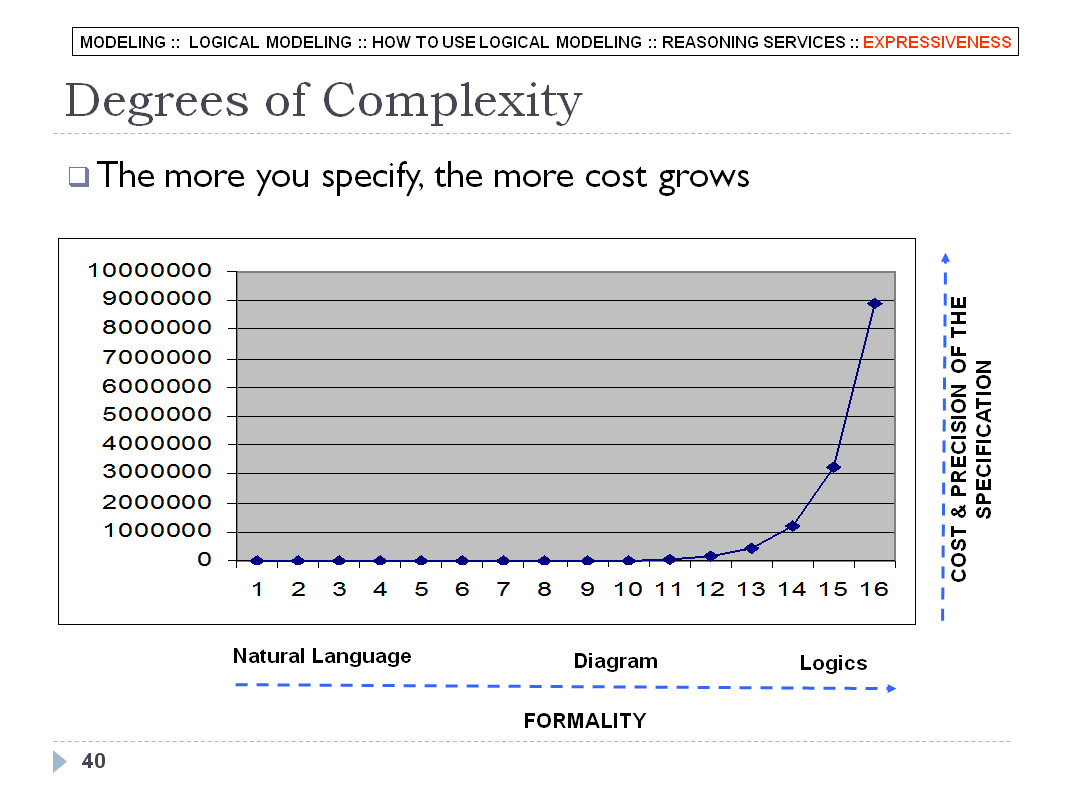
LOGICAL MODELING - SLIDE 40
LOGICAL MODELING - SLIDE 41

|